将军饮马的启示

将军饮马的启示

——线段和的最小值问题

目标

1.能用“将军饮马”问题中的轴对称思想解决线段和最小的问题,

2.通过建模思想把线段和最小这类问题转化为“将军饮马”利用“两点之间线段最短”解决问题

3.能够说明最短的理由

重点：将线段和问题转化为“将军饮马”问题

难点：1.利用轴对称的性质在定直线作出使得路线最短的点

     2.说明最短的理由

一：触发思考——基本模型（将军饮马）

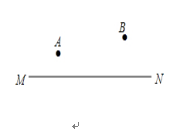
如图1，直线l表示草原上的一条河流，一骑马将军从A地出发，去河边让马饮水，然后返回位于B地的驻地.他应沿怎样

的路线行走，使路程最短？请作出这条最短路线.

            

启发探究一

 如图2，E是边长为8的正方形ABCD

边BC上一点，BE=2，P是对角线BD上的一

个动点，则PB+PE的最小值是___________．

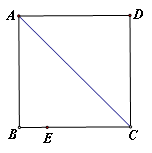
                             图2

中考链接

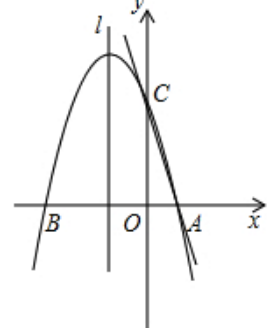
2014眉山）如图5，已知直线y=-3x+3与x轴交于点A，与y轴交于点C，抛物线y=ax2+bx+c经过点A和点C，对称轴为直线l：x=-1，该抛物线与轴的另一个交点为B．

（1）求此抛物线的解析式；

（2）点P在直线l上，求出使△PAC的周长最小的点P的坐标；

变式

粮草告急，国王命令将军带领军队从A处出发去往OM处搬运粮食，再带着粮食到ON处抓鱼，然后一起带回A处，兵贵神速，将军如何走才能最快将粮食和鱼带回A处

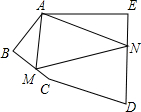
中考链接   如图,在五边形ABCDE中, ，,

AB=BC，AE=DE，在BC, DE上分别找一点M,N,使得△AMN的周长最小时，

求的度数.

启发探究二

基本模型

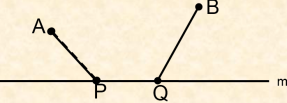
A、B为两矿山，在道路m上建两个转运站P、Q，且PQ=a，确定P、Q的位置，使AP+BQ+PQ最小。

（思考方向：将“两定点两动点”问题转化为“两定点一动点”问题）

生发探究

（2010天津）如图，在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A,B分别在x轴，y轴的正半轴上，OA=3，0B=4，D为边OB的中点

（1）若E为边OA上的一个动点，当ΔCDE的周长最小时，求E点的坐标；

（2）若E,F为边OA上的两个个动点，且EF=2，当四边形CDEF的周长最小时，求点E,F的坐标

总结：

模型