三角函数的应用

.5三角函数的应用

学习目标:

1、学生能够根据题意画出图形，根据图形找到已知和未知，以及已知和未知之间的关系

2、将实际问题转化为解直角三角形的问题（如果没有直角三角形，需要做辅助线构造直角三角形）

3、根据直角三角形元素之间的关系，利用三角函数求出问题的解

学习重点

1.经历探索船是否有触礁危险的过程，进一步体会三角函数在解决问题中的作用.

2.提高学生数学应用意识和解决问题的能力.

学习难点

根据题意，了解有关术语、准确地画出示意图, 将实际问题转化为数学问题.

教学过程

（一）触发：问题情境，提出问题

问题1、若一艘轮船沿直线航行需要经过一个小岛附近，已知在小岛周围15海里有暗礁，请问你怎样判断轮船是否有触礁的危险？

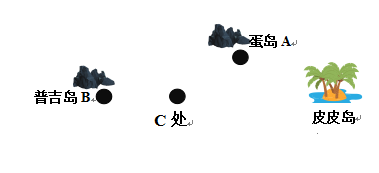
问题2：已知普吉岛B位于蛋岛A南偏西55ﾟ处，我们的船从普吉岛由西向东行驶20海里后，到达c处，C处位于蛋岛的南偏西25ﾟ方向，如果不改变方向继续前进有没有触礁的危险?

(二）启发：问题解决，形成策略

皮皮岛上有一座佛塔.在A处仰望塔顶,测得仰角为30ﾟ,再往塔的方向前进50m至B处,测得仰角为60ﾟ,那么该塔有多高?(。身高忽略不计,结果精确到1m).

（三）掘发：方法应用，凝炼思想

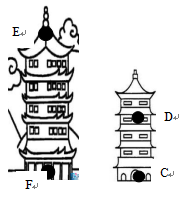
从塔底C到达了佛塔上的D点后，发现一座更高的佛塔。此时望向对面的佛塔塔顶E时仰角为62ﾟ，望向塔底F的俯角为51ﾟ。已知EF=62米，同学们能计算两塔的地面距离为多少吗？

（参考数据：sin51°≈0.8,cos51°≈0.6,tan51°≈1.2,sin62°≈0.9,cos62°≈0.5,tan62°≈1.9）

（四）归纳整理，创新思维

总结：

（课外拓展）

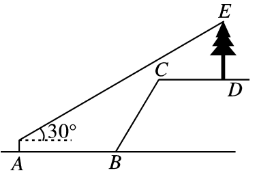
如图，小周站在A处，他的对面有一斜坡BC（坡度i=12:5）,现测得小周所站A处到斜坡底端B的距离AB=15米，坡面BC长为13米。在斜坡顶端C不远处D有一棵树，测得CD=10米，小周看树的顶部E的仰角为30，此时小周眼睛到地面的高度为1.8米，则数的高度DE约为（精确到1米）